Sistem Persamaan Linear
Sistem Persamaan Linear atau biasa disingkat SPL adalah sekumpulan persamaan linear yang terdiri dari beberapa variabel. Dalam menyelesaikan SPL, kita bisa menggunakan matriks. Ada beberapa metode yang bisa kita gunakan, seperti Eliminasi Gauss, Gauss Jordan Tereduksi, dan Crammer. Sebenarnya masih banyak metode yang bisa kita gunakan. Namun, kali ini saya hanya akan membahas 3 saja.
1. Eliminasi Gauss
Eliminasi gauss ditemukan oleh Carl Friedrich Gauss, metode ini dapat dimanfaatkan untuk memecahkan sistem persamaan linear dengan mengubah spl menjadi bentuk matriks, matriks tersebut lalu diubah kebentuk matriks segitiga atas melalui Operasi Baris Elementer. Kemudian sistem diselesaikan dengan substitusi balik.
Contoh :
Langkah 1 : UBAH SPL menjadi MATRIKS
Langkah 2 : UBAH MATRIKS menjadi MATRIKS SEGITIGA ATAS dengan METODE OBE
2. Gauss Jordan Tereduksi
Cara pengerjaannya sama dengan Eliminasi Gauss, namun setelah diubah menjadi matriks, matriks tersebut diubah lagi menjadi matriks identitas.
3. Crammer
Langkah 1 : Ubah SPL menjadi Matriks
Langkah 2 : Cari determinan matriks A
Langkah 3 : Cari determinan matriks A1 dengan mengubah kolom pertama menjadi matriks B
Lakukan hal yang sama pada A2 dan A3
Langkah 4 : Masukkan ke rumus
1. Eliminasi Gauss
Eliminasi gauss ditemukan oleh Carl Friedrich Gauss, metode ini dapat dimanfaatkan untuk memecahkan sistem persamaan linear dengan mengubah spl menjadi bentuk matriks, matriks tersebut lalu diubah kebentuk matriks segitiga atas melalui Operasi Baris Elementer. Kemudian sistem diselesaikan dengan substitusi balik.
Contoh :
Langkah 1 : UBAH SPL menjadi MATRIKS
Langkah 2 : UBAH MATRIKS menjadi MATRIKS SEGITIGA ATAS dengan METODE OBE
baris pertama tidak perlu diubah, baris kedua dan ketiga kolom pertama ubah menjadi nol dengan rumus seperti pada gambar.
ubah baris ketiga kolom kedua menjadi nol juga agar menjadi matriks segitiga atas.
Soal diatas tidak memiliki solusi karena :
Cara pengerjaannya sama dengan Eliminasi Gauss, namun setelah diubah menjadi matriks, matriks tersebut diubah lagi menjadi matriks identitas.
3. Crammer
Langkah 1 : Ubah SPL menjadi Matriks
Langkah 2 : Cari determinan matriks A
Langkah 3 : Cari determinan matriks A1 dengan mengubah kolom pertama menjadi matriks B
Lakukan hal yang sama pada A2 dan A3
Langkah 4 : Masukkan ke rumus






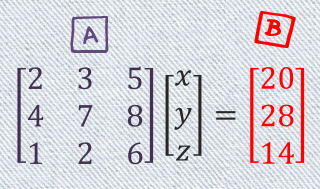







Komentar
Posting Komentar