Sifat-Sifat Determinan Matriks dan Dekomposisi
A. Sifat-sifat Determinan Matriks
1. Jika sebuah matriks berbentuk bujur sangkar, determinan matriks tersebut sama dengan determinan matriks transpose-nya. Contoh :
2. Jika dua matriks berordo sama dikalikan maka determinan matriks tersebut :
3. Jika dalam sebuah matriks terdapat baris atau kolom yang semua elemennya nol maka determinannya bernilai nol. Contoh :
4. Jika matriks berbentuk segitiga atas yang berordo nxn dimana diagonal utama tak nol maka :
5. Jika matriks B diperoleh dari matriks A dengan cara mengalikan sembarang
baris
atau kolom dengan konstanta (k) tak nol, maka :
Contoh :
6. Jika matriks B dihasilkan dari matriks A setelah baris/kolomnya ditukarkan, maka :
Contoh :
7. Jika matrik B diperoleh
dari A dikalikan
sembarang
baris atau kolom dengan konstanta
k tak nol dan hasilnya
dijumlahkan pada baris/kolom yang lain,maka :
B. Dekomposisi Matriks Crout
C. Dekomposisi Matriks Doolittle
Dekomposisi matriks Doolitle merupakan kebalikan dari dekomposisi matriks Crout.
Rumus perhitungannya :

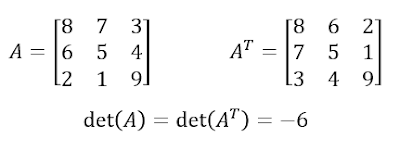





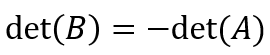






Komentar
Posting Komentar